معلومات عن حدسية ريمان

معلومات عن حدسية ريمان، يمكنك حل مشكلة واحدة فقط حتى تصل إلى المليون، لكن هذه المشكلة تختلف عن بقية المسائل الرياضية التي نعرفها، وفرضية ريمان أو تخمين ريمان هي إحدى تلك المشكلات المعروفة بمسائل الألفية التي تم تحديدها، من معهد كلاي للرياضيات في عام 2000 وحددت جائزة نقدية قدرها مليون دولار لحل أي من هذه القضايا السبع.

فرضية ريمان

كانت نظرية فيرمات واحدة من المشكلات الرئيسية في الرياضيات والمشكلة والفرضيات الأكثر شهرة وإثارة للجدل حول العالم ، ولكن تم استبدالها بفرضية ريمان بعد أن تم حل نظرية فيرما من قبل اثنين من علماء الرياضيات في التسعينيات.

لكي نتمكن من فهم فرضية ريمان ، يجب علينا أولاً معرفة دالة زيتا الخاصة بريمان ، حيث إنها وظيفة لتحديد القيمة المحددة لكل رقم ، وتحديد العلاقة التالية ، كما هو موضح في الصورة ، قيمة كل رقم.

حيث اقترح ريمان أنه من الممكن استبدال القيمة s في الدالة بأرقام صحيحة أو حقيقية وأيضًا من الممكن استبدالها بأرقام مركبة ، لأن الأعداد المركبة هي أرقام بسيطة يمكن أن تتكون من صدع حقيقي وخيالي وهو -1√ ، يتم الإشارة إلى الأرقام المركبة بالرمز (i).

عندما تتخيل خط الأعداد الحقيقي الذي نرسمه على شعاع مترامي الأطراف مركزه صفر وموزع بالأرقام من 1 إلى ما لا نهاية للأرقام الموجبة والجانب الآخر -1 إلى ما لا نهاية للأرقام السالبة ، كل هذه الأرقام موضوعة على خط اللانهاية وعلى القيم الموجبة والسالبة التي يتم توزيعها هي أرقام حقيقية ، ولكن دعنا نرى ما إذا كنا نريد إضافة أرقام معقدة إليها كيف سيكون التمثيل.

معلومات عن حدسية ريمان

كما نلاحظ من النقطة الموضحة في الصورة ، إنها نقطة بين الأعداد المركبة والأرقام الحقيقية ، والتي تساوي (2 + 3i) ، اعتقد ريمان في البداية أنه من الممكن استبدال S بأي رقم من الأعداد الحقيقية 2 أو 3 أو 4 أو 5 وما إلى ذلك ، حتى تقترب النتيجة من قيمة معينة يمكننا تحديدها ، مما يعني أن الوظيفة تعرف ببساطة كل هذه القيم.

سرعان ما أدرك ريمان خطأه ، حيث أن أي قيمة (ق) تنتج قيمة محددة من زيتا ، وهذا طالما أن S تقع على الجانب الأيمن من الخط العمودي الذي يمر عبر الرقم واحد وهذا يعني أن أي رقم تعني القيمة أعلى من واحد أن الوظيفة محددة بالزيتا ، وإلا فإن هذا يعني أن الوظيفة غير محددة.

وجد ريمان بطريقة ما طريقة تمكنه من توسيع الأعداد التي يمكن أن تجعل الوظيفة معروفة حتى لتشمل المستوى بأكمله ، ولكن على الرغم من ذلك ظلت الوظيفة غير محددة عند نقطة معينة ، وهي النقطة الأولى ، وعلى الرغم من سهولة الرقم. واحد بالإضافة إلى ذلك ، الضرب والقسمة ، في هذه الوظيفة ، إنها مشكلة كبيرة لم يحلها علماء الرياضيات بعد ، والشيء المضحك هو أن النقطة (i) ، نقطة على خط الأعداد المركبة ، عندها ستكون الوظيفة محددة ، ولكن عند النقطة الأولى لن تكون معروفة.

سؤال المليون دولار لريمان

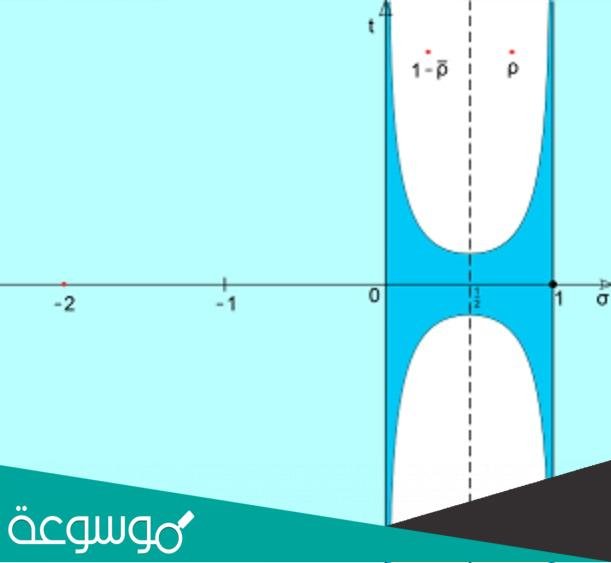
ولكن بعد كل هذا ، ما هو السؤال الذي يساوي مليون دولار ، والسؤال ببساطة (ما هي أصفار الدالة) أو ما هي القيمة التي يمكننا التعويض بها داخل الدالة لجعل قيمة الدالة تساوي صفرًا؟ هناك أرقام تجعل الدالة مساوية للصفر وهي الأعداد الزوجية السالبة -2 ، -4 ، -6 وما إلى ذلك ، هذه الأرقام تجعل الدالة تساوي صفرًا ، لكن السؤال لم يكن بهذه الصورة ، فهو يريد أصفار أخرى للدالة ، لذا فإن ريمان لن يترك السؤال بهذه البساطة.

ووضع ريمان منطقة بها جميع الأصفار غير الواضحة الأخرى، وتقع هذه المنطقة بين النقطة صفر والنقطة واحد على الخط العمودي.